In Plain Light 02.17 – The travel issue

Welcome to this month's newsletter!

In this issue:

You may want to rotate your phone in order to improve your browsing experience on this site.

Finding your way on the 'Net

If you are like me, you like to travel. I try to spend my holidays travelling (and taking pictures!) whenever I can.

Sometimes it's a fully organised tour, the kind when you don't have to care about anything.

At other times, the trip is made up of several components booked with different operators. Then it requires some planning, especially if there is more than one location involved.

Last year I spent two and a half weeks hiking in Switzerland and Italy, staying on both sides of the border. I'd say, knowing in advance how to get from one hotel to another was sort of priority. (Disclaimer: I don't drive.)

The problem: Google wouldn't help. Here's the actual location with both places, barely 35 miles apart:

Actually, there is a scheduled bus service across the border. It runs every hour following the very same route suggested by Google's driving directions and requiring one change: click here to open it in a new window.

Only, Google is unaware of it.

How come? I mean, with Google quasi owning the web, how is it possible that they can't present the information available from another source?

That's a good question which deserves some investigation.

Putting science to work

The task of finding a possible route between two given locations in a network of interconnected points is a classic problem of graph theory.

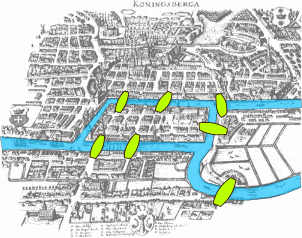
The theory is an area of mathematics, a relatively young one. Its principles were laid out by Leonhard Euler in 1736, for the Seven Bridges of Königsberg problem.

The problem sought a path over the town bridges crossing every one of them exactly once. Euler prooved that such path didn't exist. (You are still invited to have a go at it.)

The network itself represents a graph. Its points are called nodes, or vertices, and connections between them go by the name of edges. When edges are assigned costs associated with traversing them, be it travelled distances, required time, or real money spent, the graph becomes weighted.

A route travelled between two nodes in a weighted graph requires paying the costs along its edges. The best route not only gets you from A to B, but does it with the minimum cost.

Alas, this problem in its most general form is impossible to solve without trying all possible routes and comparing their costs. However, humans are surprisingly good at finding a good enough solution when presented with a number of possible options.

That is, when they get a chance to choose.

Easy riding

Some networks are easier to navigate than others.

Consider, for example, a road network. Depending on the detail level, its nodes can represent settlements, tank stations, junctions, exits, and so on. Edges between them are the actual road stretches which have, in principle, only two weights associated with them, distance and speed limit. As soon as a physical route from A to B is found, these will suffice to calculate the total distance, time needed, and [fuel] costs involved.

Most important, the journey can commence at any time.

Within city limits, the exact time of travel does play a role, though. During peak hours, when commuters drive to or from work, some edges in the network become weighted differently, as jams along them reduce their speed limit to a crawl.

Driving directions are the easiest to provide, given the road map is present in sufficient detail. This is most definitely true for Google with their maps.

Flying high

It gets more complicated with flights. Nodes are clearly airports, but what are the edges?

The answer is, direct flights. Every service connecting two airports is an edge. Its attributes, like duration and (class-dependent) price, are the weights. There are, however, other constraints which need to be taken into account, for example, the schedule details and the availability.

If you want or have to fly Monday morning, a flight going out on Tuesdays, Thursdays and Saturdays would be of little use to you. The same is true for seasonal flights unavalaible on date of your departure, obviously. Or flights which are fully booked at the time of your request.

Unlike with road networks, this information about existing connections is proprietary to their providers and distributed among them.

If you (hopefully) know your start and destination, the date and the time of day, any airline will tell you if it, eventually together with its partners, will be able to serve you.

Booking sites, just like human travel agents, don't store this information. If you ask for a flight, they send your request to different airlines and/or travel systems, such as Amadeus, and present to you all the results they get on the fly (ahem).

The procedure is facilitated by standards – for both request and response – established in the travel sector years ago.

Google's approach to offering tickets is the same. However, it is not the best.

When booking flights, it is essential to look at several places, for several reasons.

Since airlines stopped paying commissions to travel agents, the latter have been making a living by charging the customers, that is, us. This is true for booking sites as well.

As with the brick-and-mortar businesses, online vendors ask different prices for their services, meaning that you will pay a different total for the same ticket bought through different sites.

This led to uber-marketplaces comparing ticket prices offered by various sellers and the airlines themselves. Consulting them is arguably the most convenient way to shop for flights.

Getting down to earth

Finding out how to move around after you landed at your destination is the most difficult part of your planning, especially if you find yourself east of the Atlantic.

The reason is simple; there is too much choice. The Old World has a huge public transport network.

There are myriad nodes in the graph, and even more edges connecting them.

As with flights, the information about existing connections between two places is stored in different locations, and these locations don't even know about each other's existence.

In Germany, you can fly, ride by train or by bus between Frankfurt and, say, Munich, but you won't find a site which will present you with all the options, let alone offer them for sale.

What's the problem?

Well, there are several, the main being the diversity.

There is no standard for data storage and presentation
Many companies don't provide interfaces to access the information about their services in real time
There is just too much of everything

It is perfectly understandable that Google wouldn't present public transport options between two tiny towns in a European backyard. But if it's hard to blame them for their inability, their ignorance seems ... strange, to say the least.

Rome2rio of Melbourne, Australia – see the frame above and find the link below – have been creating a unique database for all types of public transport anywhere in the world.

I'll bet you, the small company is not nearly as resourceful as Google. Still, they even offer a public interface to query their database.

The offer holds for everybody, Google included.

Useless knowledge: Tea in the mountains

The other day I caught myself reviewing my old photographs from Ladakh. They are still online, if not in plain sight and not easy to find.

I was surprised to rediscover the accompanying texts.

I stopped providing the notes soon after switching to my current camera, the XPan. For one, scanning panoramas became very time-consuming on its own, and the space I'd used before dwindled away due to the larger pictures.

The trip to Ladakh was the last one before the switch, so there are still book citations and comments along with the images. For German pages, I took the trouble to translate them from English, and even included a calculator for the boiling point of water depending on the altitude.

Without getting into much detail, the air pressure diminishing with the altitude allows the steam to escape at a lower temperature than at sea level.

This was prompted by a discussion which had arose in our highest camp during the trekking. I'd promised to provide a formula after our return, so there it was, together with the derivation and a simple application based on it.

In 2006, app wasn't a word yet.

Here it is now, translated into English and supplemented by the choice of units:

If you are curious, here's how it originally appeared in German; click on the more link ("mehr") for the popup. I think formulas still look astounding, considering it's HTML and CSS only.

Now, this is truly useless, so I wonder: Where did I take the time?? 😕

Tags: #inplainlight #travelplanning #publictransport

Useful links for planning your journey online

Rome2rio: Going from Rome to Rio? From Panama City to Anguilla? From Victoria Falls to Maputo? By planes, trains and automobiles? Ask the most comprehensive connection database out there.
KAYAK: A global price integrator with sites available in over 40 countries and 20 languages. Your query will be forwarded to airlines and other travel sites to get you the best possible deal. Don't know where to go yet? Ask to get you anywhere based on your budget.
European railways: DB (Germany), SBB (Switzerland), ÖBB (Austria): Great for planning your travel around Europe by rail, as well as by bus^* and ferry in respective countries. Provide your start and destination points as street addresses and get directions also for city buses, walks and taxi rides.
^*Where train is unavailable, not as alternative.

Following issue

03.17 – The marketing issue: This issue is about creating your brand and marketing your work, told by those who've been there and done exactly that.

Unattributed images on this page are sourced from public domain via Pixabay and Wikimedia Commons.